Technosophia Community > Blog > Bilim > Öklid Mi, O Da Kim?

Öklid Mi, O Da Kim?

Kasım 28, 2020 Technosoph Bilim

Sanırım yukarıdaki soruyu geometri veya matematik dersinde (evet, birçoğuna göre o ”Bitse de çıksak!” dediğimiz dersler :)) kendinize en azından bir kere de olsa sormuşsunuzdur: Öklid de kim ola acep? Gelin de bütün eğitim hayatımız boyunca matematikte başımıza dertler açan ve Raffaello’nun meşhur Atina Okulu freskinde resmedilen şu adamı, Öklid‘i, biraz tanıyalım.

Raffaello’nun Atina Okulu freskinde Öklid’i öğrencilerine ders anlatırken görüyoruz.

(Yazarın notu: Resme bakınca aklıma ortaokuldaki çılgın matematik öğretmenim gelir. Ne günlerdi be!)

MÖ. 300 yılları civarında İskenderiye’de doğdu Öklid. Öklid, daha sonra Platon tarafından kurulan Akademi’de eğitim gördü. En büyük ünü ise birçok ispat ve teorem içeren ”Öğeler ya da Elementler” eseridir.

Michael H. Hart kitabında ”Elementlerin önemi, ispatladığı teoremlerde yatmaz. Kitaptaki teoremlerin hemen hepsi Öklid‘den önce bilinen, hatta çoğu ispatlanan teoremlerdi. Öklid‘in konuya katkısı, eldeki malzemeyi düzenleyiş ve kitabın genel planını ortaya koyuş tarzıydı.” devamında ”…teoremleri birbirleriyle bir mantık zinciri oluşturacak şekilde diziyordu.”**

Öklid elindeki veriyi düzenlemiş, öncelikle aksiyomları belirtmiş ve bir mantık sırasıyla teoremleri Elementler kitabında ispatlamıştır. Kuşkusuz böyle bir şeyi yapmak büyük bir deha gerektirir. 2000 yıldan fazla bir sürede ders kitabı olarak okutulması başarılı bir kitap olduğunu destekler nitelikte. Şimdi ise biraz Elementler kitabından örnek vermek istiyorum. Böylece konu daha anlaşılır olacaktır.

Elementler Kitabı Tanımlarla Başlar.

Örneğin,

1. Nokta, büyüklüğü olmayandır.

2. Çizgi, eni olmayan uzunluktur.

3. Bir çizginin uçları noktalardır.

4. Doğru, üzerindeki noktalara göre eşit olarak yatan çizgidir. vs.

Sonra belitlerle (aksiyomlarla) devam eder. Örneğin;

1. Herhangi bir noktadan başka herhangi bir noktaya bir doğru çizilebilir.

2. Bir doğru istenildiği kadar yine bir doğru olacak şekilde uzatılabilir.

3. Herhangi bir merkez ve bir uzunluk verildiğinde bir çember çizilebilir.

4. Bütün dik açılar benzerdir. vs.

Kitap önermelere geçmeden önce ortak kavramlardan da bahseder. Örneğin:

1. Aynı şeye eşit olan şeyler birbirine de eşittir.

2. Eğer eşit olan şeylere eşit şeyler eklenirse bütünler de eşittir.

3. Eğer eşit şeylerden eşit şeyler çıkarılırsa kalanlar da eşittir.

4. Birbiriyle örtüşen şeyler eşittir. vs.

Kitap bundan sonra önermelere geçer. Bunu kitaptan örnek bir önermeyle gösterelim.

Önerme: Verilen bir doğru parçası üzerine eşkenar bir üçgen çizmenin yolu.

Verilen doğru parçası AB olsun.

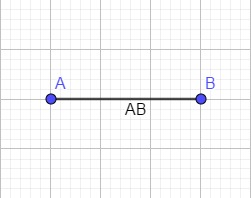
Böylece AB doğru parçası üzerine eşkenar bir üçgen çizilmesi istenmektedir.

– A merkezli ve AB yarıçapında BCD çemberi çizilsin,

– yine B merkezli AB yarıçapında ACE çemberi çizilsin,

– ve çemberlerin birbirini kestiği noktaya C noktası densin,

– C noktasından A noktasına AC doğrusu ve C noktasından B noktasına BC doğrusu çizilsin.

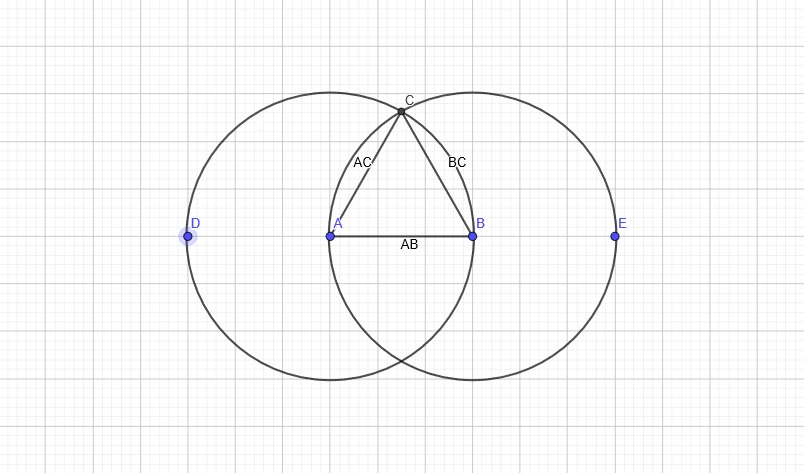
A noktası BCD çemberinin merkezi olduğu için AC, AB’ye eşittir. Yine B noktası ACE çemberinin merkezi olduğu için BC, AB’ye eşittir. AC’nin AB’ye eşit olduğu ve BC’nin de AB’ye eşit olduğu kanıtlanmıştı. Öyleyse AB=AC=BC’dir. Öyleyse ABC üçgeni eşkenardır ve verilen AB doğru parçası üzerine çizilmiştir. Tam olarak yapılması istenen de buydu.***

Aslında bu önerme ile Öklid‘in Elementleri nasıl bir akıl yürütme ve mantık dizisi ile oluşturduğunu görebiliyoruz. ”Elementler… Çıkarsama ile sonuca ulaşma (didaktik) yönteminin olağanüstü bir özelliğidir ve bu özelliğiyle yazıldığı günden bu yana düşünürleri büyülemektedir.”****