Technosophia Community > Blog > Bilim > Oyun Teorisi

Oyun Teorisi

Nisan 16, 2021 Technosoph Bilim

Oyun teorisi, taraflardan birinin çıkar sağlayabileceği herhangi bir durumda, tarafların alabilecekleri aksiyonların ve izleyebilecekleri stratejilerin olası sonuçlarını matematiksel olarak analiz edip onları bu karara yönlendiren davranışları inceleyen bir teoridir. Bu teorinin çalışmaları, pek çok ekonomik kuramın dayandığı “İnsanlar rasyonel karar alırlar.” ilkesine dayanır. Ancak oyun teorisinin kapsama alanı ekonomiden çok daha geniştir. Sevgilinizle ettiğiniz kavgalardan tutun da evinizdeki temizlik işlerini yapma sıranız dahi bu kuramın çalışma alanına girer. Ayrıca sosyal durum teorisi, evrimsel oyun kuramı gibi çeşitli şekillerde adlandırılarak biyoloji, etik, siyasi bilimler ve yapay zekâ gibi pek çok alana uyarlanmıştır.

Ortaya Çıkışı

Oyun teorisi adıyla olmasa da evlilik konusundaki seçimlere dayanan ilk çözümlemelerin 500’lü yıllarda, toplum hayatına yönelik düzenlemeler getiren Talmud Bavli (Babil Talmudu) metinlerinde Babil Yahudileri tarafından yapıldığı görülmektedir. Sonraki tarihlerde pek çok kişi, insan davranışlarının analitik çözümlemesine katkıda bulunmuştur. Ancak modern oyun teorisinin postulatlara dayalı ilk biçimi 1928 yılında matematikçi John von Neumann tarafından ortaya atılmıştır. İlerleyen yıllarda bu teori farklı bilim insanları sayesinde geliştirilmiş ve etikten bilgisayar bilimlerine kadar çeşitli alanlarda uygulanmaya başlamıştır.

Gelişimi

Von Neumann, kazanç sağlanabilecek bir durumda kişinin kazancını maksimize etme stratejisinin belirlenebileceğini ve bu yola götüren davranışlarının matematiksel olarak analiz edilebileceğini 1928 tarihli Minimaks Teoremi’nde ortaya koydu. Bu teori pek çoklarınca Oyun Teorisi’nin çıkış noktası kabul edilmiştir. Fakat yalnızca iki kişilik ve sıfır toplamlı oyunları, yani bir tarafın kazancının öteki tarafın kaybına kesinlikle eşit olduğu ve tarafların ortak kar sağlamasının bir yolu bulunamayacağı oyunları, mercek altına aldığı için kısıtlı bulundu. Bu durum akabinde pek çok matematikçinin konuyu genişletmek adına çabalamasını beraberinde getirdi. Ayrıca o zamanlarda teorem, şu an en çok ilişkilendirildiği alanlardan biri olan ekonomi ile henüz bağdaştırılmamıştı. Daha çok sosyal insan ilişkilerinde davranış stratejisini hedef alıyordu. Teoremin ekonomi ile olan ilişkisi 1938 yılına, Neumann ile ekonomist Oskar Morgenstern’in tanışmasına kadar kurulamadı. 1944 yılında ise ikilinin yayınladığı Oyun Teorisi ve Ekonomik Davranış kitabıyla Oyun Teorisi’nin tanımı genişletildi. Böylece ekonomi ile aralarında bir bağ kuruldu.

Nash Dengesi

Biraz önce değindiğimiz üzere, Oyun Teorisi’nin ilk halinde eksik ve geliştirilmeye muhtaç pek çok nokta bulunuyordu. John F. Nash, bu teoreme en büyük katkıyı yapanlardan biriydi ve bu çalışmaları ona Nobel Ödülü’nü kazandırdı. Nash, teoremin ilk halinde iki ile sınırlı olan kişi sayısını genişletti. Teorem üzerine kurulu problemlerin pek çoğunun ana hedefi olan denge noktasının, yani oyunda her tarafın kazancının maksimum olduğu bir durumun varlığının, garanti edilebileceğini ispatladı. Bu yaklaşımında Nash, Adam Smith’in aksine, “Herkesin kendi adına en yüksek kazancı elde etmek için çabalaması halinde tarafların çıkarları birbiri ile çatışacak ve denge kurulamayacaktır.” görüşünü benimsedi. Ona göre oyunu dengeye ulaştırmanın yolu, kişisel çıkarlara odaklı çabalamalardan ziyade özgeci bir strateji izlemek. Ayrıca ötekilerin de amacına hizmet etmekti.

Nasıl İşler?

Kar Dengesi

Aynı yerleşkelerde bulunan iki sabun şirketi hayal edin. Bu şirketler anlaşmasız olsun; yani belirleyecekleri fiyat için birbirleri ile görüşmeksizin kendi karlarına göre aksiyon alsınlar. Böylece sabunlarına düşük ve yüksek olmak üzere iki şekilde fiyat biçebiliyor olsunlar. Bu iki şirket de kar-zarar kayıtlarını kontrol ettiklerinde yüksek ve düşük fiyat vermeleri durumunda müşterilerin talep artışına bağlı olarak şekilde verilen karı elde ettiklerini görüyorlar.

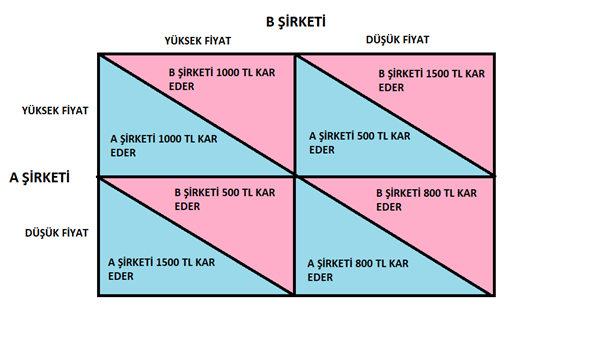
Böyle bir durum karşısında bireysel olarak seçilebilecek en iyi strateji hangisidir?

A Şirketi adına düşünelim: A Şirketi yüksek fiyat verdiği zaman, B Şirketi’nin sabunlarına biçeceği fiyata bağlı olarak ya 1000 TL ya da 500 TL kar ediyor. Düşük fiyat verdiğinde ise yine B Şirketi’nin kararlarına bağlı olarak 1500 ya da 800 TL kar ediyor. B Şirketi hangi kararı verirse versin A Şirketi adına iki durumda da daha çok kar sağlayacak olan seçenek şüphesiz ki düşük fiyat vermesidir. B Şirketi açısından değerlendirdiğimizde de durumun pek farklı olmadığını görürüz. Dolayısıyla onun için de karı maksimize edebilecek seçenek düşük fiyat vermektir. Her ikisi de bu stratejiyi izleyip düşük fiyat verirse şirket başı 800 TL kar ederler. İki tarafın da düşük fiyat vermesi bu problemin anlaşmasız versiyonunda Nash Dengesi’dir. “Ama ikisi için de 1000 TL kar etmek daha avantajlı!?” dediğinizi duyar gibiyim. Evet, şüphesiz ki oligopoller olarak her ikisinin de yüksek fiyat vermesi ikisi açısından da karı daha fazla artıracaktır. Fakat unutmamak gerekir ki bu şirketlerin esas amacı kendi karlarını maksimize etmek. Eğer bu şirketlerden ikisi de yüksek fiyat vermeyi seçecek olursa, karşı tarafın karını daha çok artırabilmek için düşük fiyata geçme riski her zaman olacaktır. Bu da kendi karlarını düşüreceğinden şirketlerin tercih etmeyeceği bir seçenektir.

Peki bu şirketler anlaşmalı olsaydı sonuç değişir miydi? Eğer bu tek seferlik bir oyun olsa düşük fiyatı seçmek muhtemelen her iki taraf için de daha karlı olacaktı. Çünkü bunu seçerek büyük bir riskten kaçıp karlarını en üst seviyeye çıkarmış olacaklardı. Ancak meşhur bir oyun problemi olan Mahkum İkilemi’nin aksine, bu oyun defalarca oynanabileceği için şirketler geçmiş tecrübelerinden ders çıkararak her iki taraf için de en karlı olacak sonuca zamanla ulaşabilirler.

Peki, bu süreç nasıl işler?

• Her iki şirketin de yüksek fiyat ile piyasaya giriş yaptığını düşünelim. Bu durumda ikisi de 1000 TL kar eder.

• Bir süre sonra, şirketlerden biri kurnazlık yaparak daha fazla kar elde edebilmek adına fiyatlarını düşürür. Böylece kendi ürünlerine olan talebi artıracağı için, öteki şirketin karının azalmasına sebep olurken kendi karını artırır.

• Kendi karının düştüğünü gören öteki şirket de karşılık olarak kendi fiyatlarını düşürür ve iki taraf da 800 TL kazanır.

• Bu stratejiyi izleyerek en faydalı sonuca ulaşamayacaklarını fark eden şirketler, yüksek fiyat politikasını benimser ve karşı tarafı aldatmazlarsa ikisi için de getirisi en çok olan sonuca varacaklarının bilincinde olurlar.

Son Söz

Oyun teorisi hayatta çeşitli konulara dair aldığımız kararların sebeplerini ve farkında olmasak bile bu kararları alırken değerlendirdiğimiz etkenleri hangi kıstaslara göre mercek altına aldığımızı analiz etmede bizlere yardımcı olmaktadır. Böylece farklı problemlerde, taraflar rasyonel hareket edecek olursa hangi stratejiyi izleyebileceklerini tahmin edebilmektedir. Ayrıca yaptıkları seçimlerin doğasını da anlamlandırabilmektedirler. Bütün bu getirileriyle oyun teorisi, yaşamımızın neredeyse her alanına dokunan bir konu olduğu gibi yalnızca matematik ve ekonomide değil, pek çok bilimsel alan ve camiada da önemli bir yere sahiptir.